How To Find The Centre Of The Circle Explained — What It Means And Why It Matters

Hey there, coffee buddy! Ever stare at a perfect circle, maybe on a pizza or a perfectly drawn design, and wonder, "Where's the heart of this thing?" You know, that special spot? Well, my friend, that's the centre of the circle. And today, we're going to chat about how to find it, what it actually means, and why, believe it or not, it actually matters. No boring math lecture here, promise!
So, picture this: you’ve got a circle. It’s just… there. Round and mysterious. But like a good mystery, it’s got a solution, right? And that solution is finding its centre. It's not just some random point. Oh no. It's the absolute middle. The anchor. The VIP of the circle world.
Think of it like your favourite comfy armchair. It’s the one spot where everything feels just right, where you can relax and be yourself. The centre of a circle is kind of like that for the circle itself. It's the point from which all other points on the edge are exactly the same distance away. Pretty neat, huh?
This magical distance? We give it a fancy name, of course. It's called the radius. You’ve probably heard that one before. It’s like the circle’s "reach." How far it can stretch out from its comfy centre spot. And the line that goes all the way across the circle, passing through the centre? That’s the diameter. Twice the radius, for all you math whizzes out there!
So, How Do We Actually Find This Elusive Centre?
Alright, enough with the cozy analogies. Let's get down to business. You've got a circle, and you need to locate its beating heart. How? Don't worry, you don't need a superhero cape or a secret decoder ring. There are a couple of super-simple, tried-and-true methods.
Method number one: The Folding Technique. This is for the tactile folks, the ones who like to get their hands dirty (or, you know, just fold some paper). Grab your circular object. If it's a piece of paper with a circle drawn on it, perfect! If it's something solid, like a mug coaster, you might need to trace it onto some paper first. Get creative!
Now, carefully fold the circle in half. Make sure those edges line up perfectly. Crease it nicely. You've just created a line. That line is a chord, by the way. Fancy word for a straight line segment connecting two points on a curve. But the important thing is, the centre of the circle must lie somewhere on this line you just folded.
But wait, one fold isn't enough, is it? That centre could be anywhere along that crease. So, what do we do? We do it again! Unfold your circle. Now, fold it in half again, but this time, make sure your fold is different from the first one. Aim for a new line that also goes through the edge of the circle.
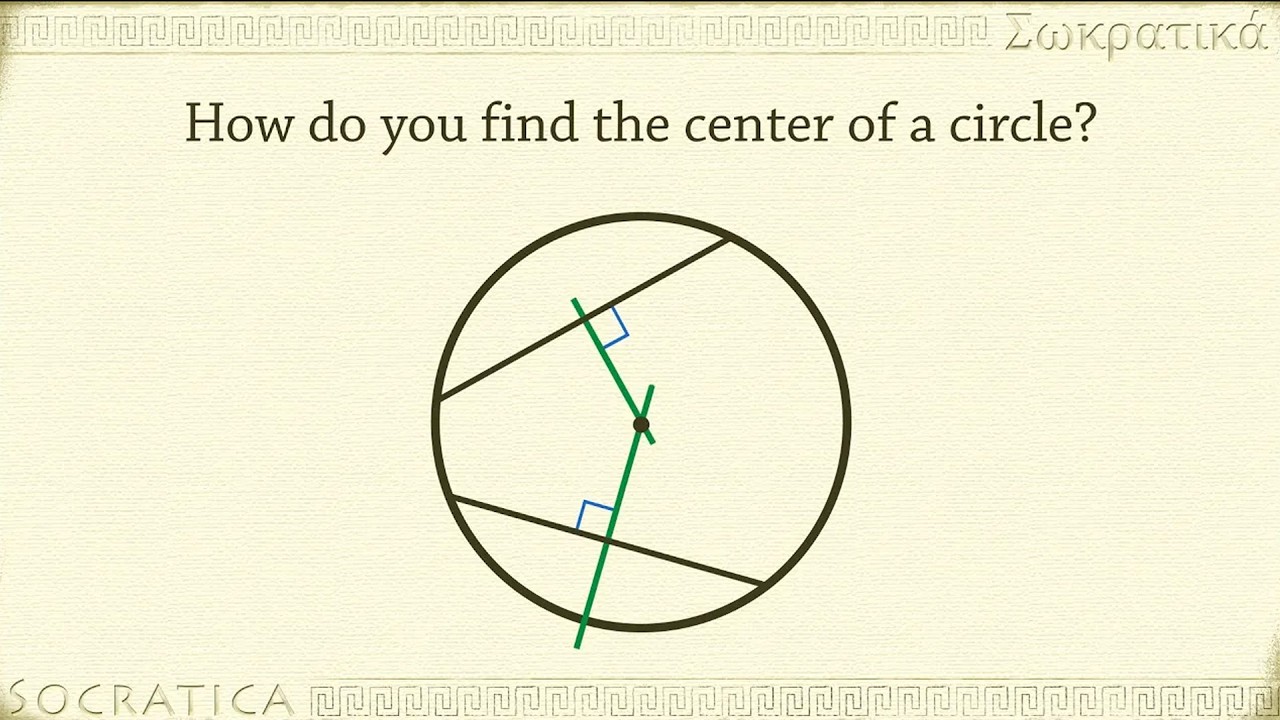
So you've got two nice, neat creases. Two chords. And guess what? The point where these two lines cross? Bingo! That's your centre. Ta-da! It’s like a geometric treasure hunt, and you just found the X that marks the spot.
Why does this work, you ask? It's all about symmetry. A circle is perfectly symmetrical. When you fold it in half, you're essentially creating a line of symmetry for that fold. The centre has to be on every single one of these lines of symmetry. So, where multiple lines of symmetry intersect, that's your centre. Simple, elegant, and totally foolproof (as long as your folding is neat, of course!).
Method number two: The Compass and Straightedge Adventure. This is for the more precise types, the ones who love their tools. You’ll need a compass and a straightedge (a ruler, essentially). This method is a bit more involved, but it’s a classic for a reason.
First, you need at least three points on the circumference of your circle. If you only have the circle itself, you can mark three distinct spots on its edge. Just eyeball it, make them spread out a bit. The more spread out they are, the easier it will be.
Now, grab your compass. Place the pointy bit on one of your marked points. Open your compass to a distance that’s more than half the distance between that point and another point. This is important! If it's too small, it won't work. Trust me on this one.
Draw an arc. Now, without changing the compass width, move the pointy bit to your second marked point. Draw another arc, making sure it intersects the first arc. You should have two little arcs crossing each other.
Repeat this process for a third point. Place the compass on your third marked point, with the same width, and draw two more arcs that intersect the ones you've already made. You’ll end up with a bunch of intersecting arcs.
Now, take your straightedge. Connect the intersection points of the arcs you made. You'll draw a line segment connecting two of the intersections, and another line segment connecting two other intersections. These lines are actually perpendicular bisectors of the chords you implicitly created between your points.
And where do these two lines intersect? You guessed it! That's your centre. It’s a bit like drawing fancy, geometric spiderwebs to find your way. Pretty cool, right?
Why does this work? Each arc you draw is essentially creating points that are equidistant from two points on the circle. The line you draw by connecting the intersections of these arcs is the perpendicular bisector of the chord connecting those two points. And guess what? The centre of a circle lies on the perpendicular bisector of any chord. So, by finding the intersection of two such perpendicular bisectors (which are formed by our clever arc-drawing), you pinpoint the centre.
It sounds complicated, but when you draw it out, it's quite satisfying. It’s like solving a puzzle, and the puzzle pieces are made of pure geometry.
What Does The Centre Actually Mean?
Okay, we’ve found the centre. We can fold our way there, or draw some fancy arcs. But what does this point signify beyond being the "middle"?

Well, as we touched on, it’s the point of equal distance. Every single point on the circle's edge is exactly the same distance from the centre. This definition is actually the fundamental definition of a circle. It's not just a round shape; it's a set of points that are all a specific distance from a central point. That centre point is the boss!
It's also the axis of symmetry. If you were to spin the circle around its centre, it would look exactly the same at any angle. It's perfectly balanced, perfectly symmetrical. Think of a spinning record on a turntable – it rotates around its centre, and it looks the same no matter how fast it spins or where you look.
The centre is also crucial for understanding the circle's properties. When we talk about the radius, the diameter, the circumference, and the area – all these measurements are directly linked to that central point. Without it, the radius is just a random line segment, and the diameter is just a chord. The centre gives them their meaning and their role.
Why Should You Care? Does It Really Matter?
Now, I know what you might be thinking. "This is all well and good, but I’m not exactly building a Ferris wheel tomorrow. Why should I care about the centre of a circle?"
Ah, but my friend, the humble circle and its centre are everywhere! You might not even notice them, but they’re silently influencing things around you.
Construction and Design: Think about laying out a circular garden bed. You need to know the centre to ensure your plants are spaced evenly. Building a perfectly round fountain? The centre is your starting point. Architects and engineers rely on understanding the centre of circular elements constantly. Even a perfectly round dinner table needs a centre to make sure everyone has enough elbow room!

Art and Craft: If you're a painter, a potter, or a crafter, you’re probably using circles all the time. Want to draw a perfect mandala? You absolutely need a centre to build out from. Making a perfectly symmetrical ceramic bowl? The potter's wheel centres your clay for a reason!
Navigation: This one might surprise you! While not directly finding the centre of a drawn circle, the concept of a central point is vital. Think about GPS. You're navigating to a specific location, which is like a central point on a map. Understanding angles and distances (which relate to circular paths) is key. Even old-school sailors used celestial navigation, relying on the predictable paths of stars, which are effectively circular in our sky.
Physics and Engineering: The rotation of planets, the spin of a turbine, the gears in a machine – they all revolve around a centre of rotation. Understanding this centre is paramount for calculating forces, speeds, and the overall efficiency of these systems. Imagine a car tire without a central hub – it just wouldn't work, would it?
Even in everyday life! When you're slicing a cake (if it's round, of course!), you're trying to cut through the centre to get roughly equal pieces. When you're aiming for a bullseye in darts or archery, you're aiming for the centre. It’s a universal concept of balance and focus.
So, you see, the centre of the circle isn't just some abstract geometric concept. It's the anchor, the point of reference, the heart that gives the circle its form, its function, and its meaning. It’s the foundation upon which so much of our world, both seen and unseen, is built.
Next time you see a circle, whether it’s on your coffee cup, a coin, or the moon (okay, maybe not the moon's centre, but you get the idea!), take a moment to appreciate its centre. It’s the silent hero, the unsung hero of roundness. And now, you know how to find it and why it’s more important than you might have thought. Pretty cool, right? Now, pass the sugar, would you? This chat has made me thirsty for more… of coffee, that is!
