Most Difficult Math Equation In The World

Hey there! So, you wanna know about the most difficult math equation in the world? Like, the one that makes even super-smart people sweat? Well, grab your coffee, or your tea, or whatever your brain-fuel of choice is. We're about to dive into something that’s, shall we say, a tad more complex than figuring out how many cookies you can realistically eat in one sitting. (And let's be honest, that's a tough one too, right?)
When you hear "most difficult," you might picture something with a million squiggly lines and numbers that look like they're doing a little dance of chaos. And you're not entirely wrong. But it's not just about looking scary, is it? It's about what it means. What it unlocks. Or, more often, what it doesn't unlock, because we haven't quite figured it out yet. Big bummer, I know.
So, what is this mythical beast of an equation? Well, it’s not a single, neatly packaged thing like, say, E=mc². That one's pretty famous, and while it's got some heavy implications, it's not exactly going to give you nightmares. No, the real tough nuts are the problems that have no known solution. Or, if they do, the solution is so incredibly intricate it makes your head spin. We're talking about unsolved problems in math. The Everest of math, if you will. And there are a few contenders for the "most difficult" crown.
The Millennium Prize Problems: The Big Kahunas
If we're talking about the most famous and highly prized difficult equations, we have to talk about the Millennium Prize Problems. Ever heard of them? No? Well, buckle up! Back in the year 2000, the Clay Mathematics Institute decided to spice things up. They picked seven enormous mathematical questions. Seven. And they said, "Hey, if you can solve one of these, we'll give you a million bucks. No biggie."
A million dollars! For solving a math problem! Suddenly, math sounded a lot more exciting, right? Like a treasure hunt, but with theorems instead of X marks the spot. The catch? These problems are insanely hard. Like, ridiculously, mind-bendingly, "I-need-a-nap-just-thinking-about-it" hard.
And here's the kicker: out of the seven, only one has been solved so far. Just one! We’re talking about the Poincaré Conjecture. Which, honestly, sounds like something you’d say after a particularly strong espresso. But it was a huge deal when it was solved. Grigori Perelman, the guy who cracked it, basically became a math celebrity. Though, apparently, he wasn't too keen on the fame and money. Weirdo, right? (Just kidding, mostly. He was a brilliant dude.)
So, that leaves us with six other Millennium Prize Problems. Six other behemoths of mathematical thought. And those are what we’re talking about when we say "most difficult." They're not just one equation, but rather deep, fundamental questions that require entire new branches of mathematics to even try and tackle.
The Riemann Hypothesis: The One That Haunts Mathematicians
Okay, let's talk about one of the reigning champions of difficulty: the Riemann Hypothesis. This one is an oldie but a goodie, first proposed way back in 1859. Yep, over 160 years ago, and still no definitive proof. Makes you wonder if Bernhard Riemann was just messing with future mathematicians, doesn't it? Like, "Here’s a little puzzle for you guys. See ya in a century!"

What's it all about? Well, it deals with prime numbers. Those sneaky numbers that are only divisible by 1 and themselves. You know, 2, 3, 5, 7, 11... they're the building blocks of all other numbers. Super important. But their distribution? It's kind of random, kind of chaotic. Like trying to predict where a squirrel is going to go next. Impossible, right?
The Riemann Hypothesis, in very simplified terms, suggests that there's a hidden order to these prime numbers. It connects them to something called the Riemann zeta function. And if this hypothesis is true, it has massive implications for number theory. Like, huge. It would unlock so many doors, explain so many patterns.
Imagine trying to understand a whole language, but you’re missing the alphabet. That’s kind of what it’s like without solving the Riemann Hypothesis. It’s like a giant key, but we can’t find the lock. Or maybe the key is just… really, really complicated. And the lock is even more so.
Why is it so hard to prove? Well, it involves complex numbers, infinite series, and a whole lot of abstract thinking. Mathematicians have thrown everything they’ve got at it. Supercomputers have crunched numbers for years, testing out billions and billions of cases. And every single one they've tested fits the hypothesis. But that’s not a proof, is it? That’s just evidence. Like finding lots of red socks in your laundry doesn't prove you only own red socks, right? You might have a sneaky blue one hidden in there somewhere.
The pressure is immense. It’s not just about personal glory; it's about advancing our understanding of the universe in a really fundamental way. So yeah, the Riemann Hypothesis is definitely a strong contender for "most difficult." It's elegant, it's important, and it's stubbornly refusing to be solved.

P vs NP: The Computer Science Conundrum
Now, let’s switch gears a bit and talk about something that affects our digital world, even if we don’t realize it. This one's called the P vs NP problem. Sounds a bit like a boxing match, doesn't it? “In this corner, weighing in with efficiency, we have P! And in the other corner, with its perplexing puzzles, is NP!”
What does P and NP even mean? In computer science terms, it’s about the difficulty of solving problems. Think about it this way: some problems are easy to solve, and some are easy to check if a proposed solution is correct. That’s the difference.
P problems are those that can be solved quickly by a computer. Like sorting a list of numbers. Easy peasy. You give a computer a bunch of numbers, and it can sort them in a reasonable amount of time. No sweat.
NP problems, on the other hand, are problems where a proposed solution can be checked quickly, but finding the solution can take a very, very long time. Think of trying to find the best way to pack a ridiculously full suitcase. If someone gives you a packed suitcase, you can probably tell if it's packed well (or if it's about to explode) pretty quickly. But you finding the absolute best way to pack it? That could take ages, especially if the suitcase is enormous and has weirdly shaped items.
The P vs NP question is basically asking: Is P equal to NP? In other words, if a solution to a problem can be checked quickly, can it also be found quickly? If P = NP, it would be a monumental shift in computer science. It would mean that many problems that we currently consider computationally intractable – meaning they would take billions of years to solve – could suddenly be solved efficiently. Think about breaking complex encryption, finding optimal routes for a massive delivery network, or even discovering new drugs. Mind-blowing, right?
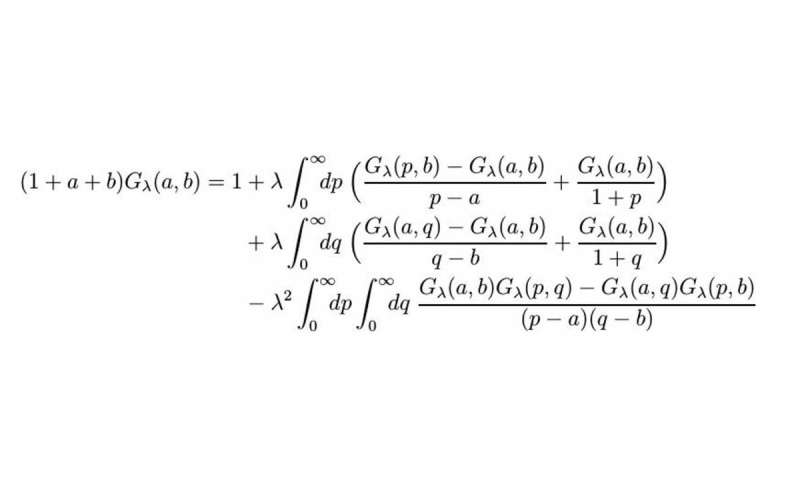
But if P ≠ NP, then these hard problems will remain hard. And that's what most mathematicians and computer scientists suspect is true. But proving it? That’s the billion-dollar question. (Literally, in the case of the Millennium Prize.)
Why is it so tough? It’s deeply theoretical. It requires a fundamental understanding of computation and complexity. We’re talking about the very limits of what computers can do. It’s like asking, "Can we build a machine that will always give us the best answer to any question instantly?" That sounds a bit like magic, doesn't it? And magic is usually pretty hard to prove.
Navier-Stokes Existence and Smoothness: Fluid Dynamics' Fiery Riddle
Let's talk about something a bit more… physical. Navier-Stokes Existence and Smoothness. This one deals with fluids. You know, water, air, that sort of thing. The equations that describe how fluids move are called the Navier-Stokes equations. They're used everywhere – in weather forecasting, designing airplanes, understanding blood flow. Pretty essential stuff, right?
The problem is, while we use these equations, we don't fully understand them in all situations. Specifically, the question is whether solutions to these equations always exist and are smooth (meaning they don't have any sudden, wild jumps or infinities) for all possible starting conditions. Imagine trying to predict the exact path of a hurricane. If the equations describing the air movement are wonky, your prediction is going to be… well, a bit of a guess.
Think about a turbulent river. The water is swirling, unpredictable. The Navier-Stokes equations are supposed to describe that chaos. But what if, under certain extreme conditions, the equations break down? What if the speed of the fluid becomes infinitely fast at some point? That would be a pretty big deal, wouldn't it? It would mean our models are incomplete. We might be missing a crucial piece of the puzzle.
Proving this involves some seriously advanced calculus and differential equations. We're talking about proving that solutions are well-behaved, even when the fluid is acting completely bonkers. It's like trying to prove that a tornado will always follow a perfectly predictable, smooth path, even though you can see it tearing everything apart. It's a big ask!
This problem is so difficult because fluids are incredibly complex systems. There are so many tiny interactions happening all at once. Trying to pin down a perfect mathematical description for every single possible scenario is like trying to count every grain of sand on every beach in the world. And doing it with perfect precision!
The Others: The Enigmatic Ensemble
We've only scratched the surface, really. Remember, there are other Millennium Prize Problems! We've got the Yang-Mills Existence and Mass Gap, which is a biggie in theoretical physics, trying to understand the fundamental forces of nature. And then there’s the Birch and Swinnerton-Dyer Conjecture**, which has to do with elliptical curves and number theory. Each one is a universe of its own, a labyrinth of concepts that would take years of dedicated study to even begin to grasp.
These aren't just abstract puzzles for mathematicians to play with. They are the frontiers of our knowledge. Solving them could unlock new technologies, deepen our understanding of the universe, and perhaps even change the way we think about reality itself. That’s why they’re called "difficult." It's not just about complex calculations; it's about fundamental questions that have eluded the greatest minds for decades, even centuries.
So, the "most difficult math equation in the world"? It’s not a single equation you can write on a blackboard in one go. It’s more like a collection of the most challenging, the most profound, the most important unanswered questions in mathematics. They are the challenges that push the boundaries of human intellect. They’re the ones that make mathematicians sigh, scratch their heads, and then dive back in with renewed determination. Because that’s the beauty of math, isn't it? Even the impossibly hard stuff can, eventually, be conquered. Or at least, we can try. And the trying? That’s where the real adventure is.
